实数是数轴上的点所对应的数,包括有理数和无理数。
实数的分类:
1、有理数,2、无理数。
有理数:可按不同标准分为:
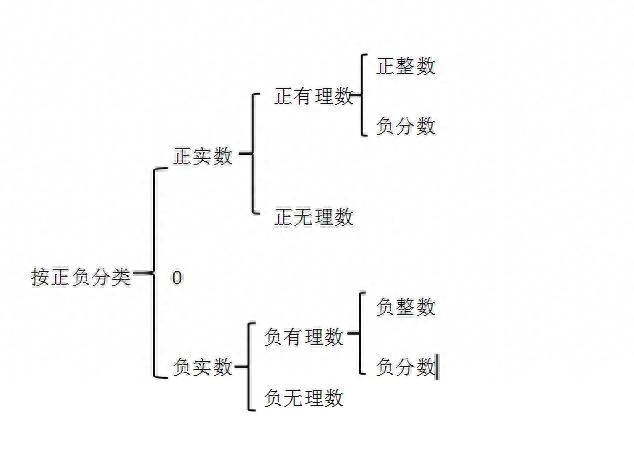
①正有理数,②零,③负有理数;
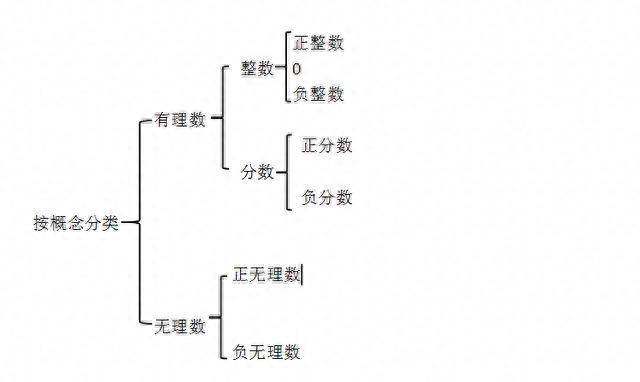
或a、整数,b、分数。
正有理数可分为正整数和正分数,负有理数可分为负整数和负分数。
整数可分为正整数、零、负整数,分数可分为正分数和负分数。
无理数:1、正无理数,2、负无理数。
有理数与无理数的区别在于:有理数是有限小数或循环小数(即有理数都可写成q/p(p、q是互质的整数)形式的分数,整数可看成分母为1的分数);无理数是无限不循环小数,无法用分数来表示。
※注:√2/2、√3/2…是无理数而不是有理数。
初中阶段所涉及的主要无理数类型:
1、具有特殊结构的无限不循环小数:
如:1.01011011101111…,0.1234567891011…
2、开方后无法被求出的数的方根:
如:√2,√3,√5…
3、具有特殊意义的数:
如:sin45,sin60,圆周率及与有关的数…
※注:无限小数不一定是无理数,但无理数一定是无限小数。
与实数相关的基础知识:
数轴
数轴是一条有原点、正方向和单位长度的直线。
数轴上的点与实数是一一对应的。
绝对值
绝对值是用来表示一个数在数轴上与原点的距离的,这个距离不可以是负数,因此一个数的绝对值也不能是负数,即|a|≥0。
相反数
两个数的符号相反并且绝对值相等的情况下,它们互为相反数,也就是说互为相反数的两个数的和为0:a+b=0。
倒数
乘积为1的两个数互为倒数,也就是互为倒数的两个数的乘积为1:ab=1。
※:0没有倒数。
科学计数法及近似数
科学计数法:科学计数法的表示形式为a10^n,其中1≤丨a丨<10,n为整数。
近似数及有效数字
四舍五入到某一位的近似数,表示它的精确度到该位。
从左边第一个不是零的数字到右边表示精确度的数字,就是这个数的有效数字。
平方根
一个数的平方等于a时,这个数是a的平方根(也叫二次方根)。
正数有两个平方根,它们互为相反数;0的平方根仍为0;负数没有平方根。
算术平方根:
一个非负数的平方根称为它的算术平方根。
三次方根(立方根):
一个数的立方等于a时,称这个数是a的立方根(三次方根),任何实数都有一个立方根,正数的立方根为正数,负数的立方根为负数,0的立方根仍为0。
实数的运算同有理数的运算规律和运算法则一样适用。